Cosa sono, come funzionano e a cosa servono gli Accelerometri

Oggigiorno abbiamo sempre più a che fare con dei minuscoli dispositivi, a noi invisibili, chiamati accelerometri. Oramai tutti gli smartphone ne sono dotati e abbiamo imparato che è grazie a questo componente che il cellulare è in grado di capire che lo stiamo ruotando e di conseguenza può eseguire tutte le operazioni di rendering necessarie per ridisegnare il contenuto dello schermo con l’angolazione corretta. Anche alcuni controller di gioco fanno uso di un accelerometro, primo tra tutti il nunchuk della Nintendo.

A dispetto di tutte queste applicazioni “ludiche”, un accelerometro è un dispositivo tanto semplice quanto sofisticato e trova la sua vera destinazione d’uso in applicazioni molto più professionali piuttosto che in un semplice videogioco. Avete presente il segway? E’ proprio grazie ad un accelerometro che questi innovativi sistemi di traporto riescono a mantenersi in equilibrio su due ruote. I dispositivi di navigazione, soprattutto quelli autonomi, anche fanno uso di accelerometri uniti a giroscopi e magnetometri. Sistemi di test, controllo e sicurezza sulle automobili e sui mezzi di trasporto in genere sono altre applicazioni che fanno uso di accelerometri.

Ma cos’è un accelerometro? E’ sostanzialmente un dispositivo in grado di rilevare o misurare un’ accelerazione, ovvero una variazione di velocità nel tempo.

Come funziona un accelerometro

Per avere uno schema mentale che ci aiuti a visualizzare in qualche modo come opera un accelerometro, immaginiamolo come costituito da una sfera al centro di un cubo, sospesa da 3 molle che la attraversano, agganciate a loro volta al centro di ogni faccia del cubo:

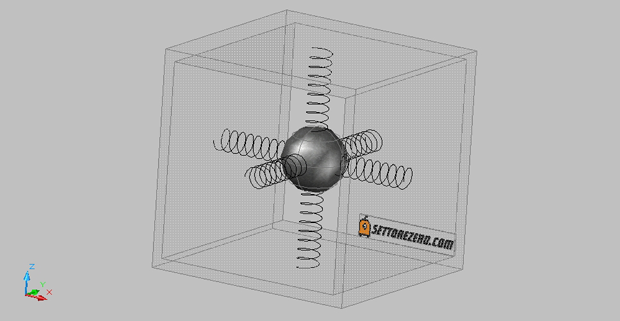
Muovendo il cubo nello spazio, la sfera si muoverà al suo interno allungando e comprimendo, di conseguenza, le molle che la tengono sospesa. La misurazione del grado di compressione delle molle permette di stabilire che c’è stata un’accelerazione (ovvero una variazione di velocità) nella direzione in cui si trova la molla compressa e quindi anche di quantificarla.

Molti accelerometri sono davvero costruiti più o meno in questo modo, anche se la massa sospesa non è sferica, le molle sono realizzate in silicio ed il tutto è piccolo come la punta di un fiammifero o meno. Si legge difatti sul datasheet di un accelerometro molto comune, l’ADXL345 prodotto dalla Analog Devices:

The sensor is a polysilicon surface-micromachined structure built on top of a silicon wafer. Polysilicon springs suspend the structure over the surface of the wafer and provide a resistance against acceleration forces

Nell’immagine 1 in realtà ho rappresentato più precisamente un accelerometro a 3 assi dal momento che la massa è attraversata da 3 molle ortogonali tra loro ed ogni molla si trova quindi nella direzione di un asse cartesiano. Con un accelerometro a 3 assi è possibile rilevare le variazioni di velocità nelle 3 direzioni dello spazio.

Gli assi di riferimento dell’accelerometro si originano al centro della sfera, per cui si possono misurare valori di accelerazione positivi o negativi in dipendenza dal verso in cui l’accelerazione è diretta.

In un accelerometro a 3 assi, la situazione nel mondo reale non sarà quella rappresentata in figura 1 ma piuttosto questa:

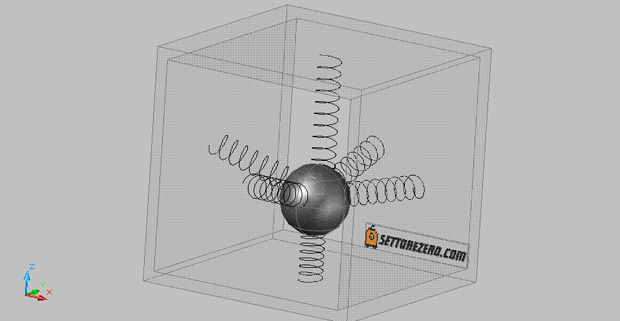
Vedete che la massa (la sfera) si trova  verso il basso e di conseguenza comprime la parte inferiore della molla orientata lungo l’asse Z. Perchè accade questo? Per il semplice motivo che qualsiasi corpo, sulla superficie terrestre, è attratto verso il basso a causa della forza di gravità.

Forza di gravità e accelerometri a uno, due, tre assi

Un corpo in stato di quiete, quindi, subisce sempre un’accelerazione verso il basso che vale 9.822 m/s² (o 9.822 N/Kg). Questo valore di accelerazione, dovuto all’interazione gravitazionale, è anche indicato come g (scritto minuscolo, per distinguerlo dalla G maiuscola che rappresenta la costante di gravitazione universale).

Si misura quindi un valore di accelerazione pari ad 1g quando la velocità aumenta di 9.822 m/s per ogni secondo (9.82 m/s² appunto).

Sui cellulari, ad esempio, non c’è bisogno di un accelerometro a 3 assi dal momento che le applicazioni che fanno uso di questo “strumento” sono sempre sviluppate su due dimensioni, per cui in questi dispositivi abbiamo generalmente un accelerometro a 2 assi. In un accelerometro a due assi non è presente la “molla” che attraversa la “sfera” lungo l’asse Z, per cui non è possibile misurare il valore di accelerazione lungo tale asse. Ok, direte voi: possiamo ruotare il dispositivo di 90°e quindi la misuriamo lo stesso, ma poi? Rimane sempre un asse “scoperto”.  Allo stesso modo esistono anche accelerometri ad un solo asse. L’utilizzo dell’uno o dell’altro tipo di accelerometro dipende sempre dalla destinazione d’uso. Ovvio che un accelerometro a 3 assi costa più di uno a due assi, per cui a volte è anche necessario fare delle considerazioni di tipo economico.

Usare un accelerometro per misurare l’inclinazione : il tilt sensing

Poco fa ho fatto l’esempio dell’accelerometro dei cellulari utilizzato per ruotare lo schermo: proprio per la sua caratteristica di essere “affetto” dalla forza di gravità, un accelerometro, oltre che per misurare il valore di accelerazione, può anche essere utilizzato come dispositivo per misurare l’inclinazione di un corpo, anzi questo è forse il suo utilizzo più diffuso.

L’accelerometro, difatti, proprio per come è realizzato, è in grado sia di misurare l’accelerazione statica (ad esempio quando lo ruotiamo sul posto) che l’accelerazione dinamica (ad esempio: lo fissiamo su un’automobile in corsa). Per applicazioni di tilt sensing (ovvero la misurazione dell’inclinazione di un corpo) viene appunto sfruttata la misurazione dell’accelerazione statica : assumiamo che la forza di gravità sia l’unico valore di accelerazione che agisce sul corpo, ignorando valori di accelerazione superiori ad 1g.

Si capisce, quindi, che per le applicazioni di tilt sensing non è assolutamente necessario avere a disposizione degli accelerometri in grado di misurare valori spropositati di accelerazione

Immaginiamo di ruotare il nostro cubo lungo l’asse X e tenerlo fermo con una certa angolazione: la sfera ora comprimerà due molle, quella lungo l’asse X e quella lungo l’asse Z (la molla lungo l’asse Y invece si allunga soltanto ma non risulta compressa in alcun punto, quindi diciamo che lungo l’asse Y misuriamo un valore pari a zero):

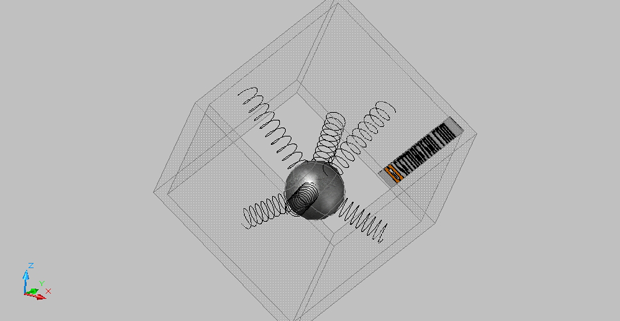
L’accelerometro ora misurerà il valore di compressione di due molle, o anche: noteremo che il valore di accelerazione lungo un solo asse vale meno di 1g per cui in entrambi  i modi di osservare l’evento si capisce che il cubo in qualche modo è inclinato. Questa assunzione è valida solo se il corpo non è in movimento, stiamo difatti tenendo conto di accelerazioni statiche, ovvero dovute esclusivamente alla forza di gravità terrestre. Misurando il valore di accelerazione lungo gli assi, facendo uso di un po’ di trigonometria, è possibile stabilire di quanti gradi è ruotato il corpo e quindi il dispositivo all’interno del quale l’accelerometro è montato.

Roll, Pitch e Yaw

Introduciamo ora altri concetti relativi alla rotazione di un corpo nello spazio, soprattutto per capire fino a che punto può essere utile un accelerometro per la misurazione dell’ inclinazione.

Un corpo può rotare nello spazio lungo 3 assi, facendo riferimento alla dinamica applicata ai velivoli si parla più propriamente di rollio, beccheggio e imbardata. Osservate questa immagine:

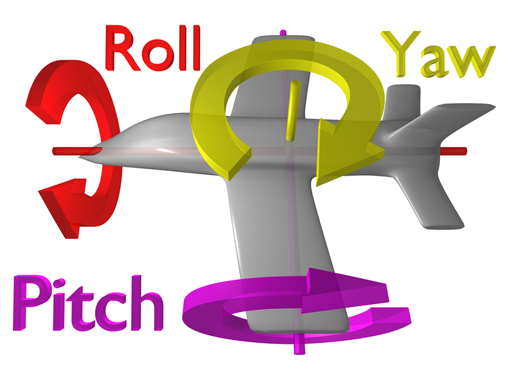
Per convenzione la rotazione del velivolo lungo l’asse X (in rosso) del velivolo si chiama rollio (Roll). La rotazione lungo l’asse Y del velivolo (in viola) si chiama beccheggio (Pitch) e la rotazione lungo l’asse Z del velivolo (in giallo) si chiama Imbardata (Yaw).

Immaginate ora che gli assi X e Y dei velivolo si trovino sul piano dell’orizzonte e l’asse Z sia perpendicolare a questo piano.

Una rotazione intorno all’asse X forma un angolo tra asse Y e orizzonte. Questo angolo che Y forma con l’orizzonte a causa della rotazione di X si chiama angolo di rollio e viene generalmente indicato con la lettera greca φ (phi minuscola).

Essendo l’asse Z ortogonale con l’asse Y, una rotazione intorno a X genera lo stesso angolo tra Z e il vettore della forza di gravità

Una rotazione intorno all’asse Y forma un angolo tra asse X e orizzonte. Questo angolo che X forma con l’orizzonte a causa della rotazione di Y si chiam angolo di beccheggio e viene generalmente indicato con la lettera greca θ (theta minuscola)

La rotazione intorno all’asse Z non porta alla formazione di nessun nuovo angolo con l’orizzonte: la rotazione intorno a Z porta piuttosto gli assi X e Y a ruotare di un certo angolo sul piano in cui già si trovano. Questo angolo si chiama angolo di imbardata e viene generalmente indicato con la lettera greca ψ (psi minuscola).

Un accelerometro a 3 assi è in grado di rilevare l’angolo di rollio e l’angolo di beccheggio ma non l’angolo di imbardata per quanto appena detto dato che la rotazione intorno a Z non provoca una variazione degli angoli che gli assi formano rispetto all’orizzonte e di conseguenza i valori di accelerazione gravitazionale cui i singoli assi sono sottoposti. Ancora non capite il perchè? Prendete il cubo dell’immagine 2, fatelo ruotare unicamente lungo l’asse Z, cambia qualcosa? La sfera all’interno si muove? Decisamente no: le molle rimangono con gli stessi valori di tensione (gli assi X e Y continuano a mantenere lo stesso valore di angolazione rispetto al piano dell’orizzonte).

Per tale motivo non è possibile usare un accelerometro nel caso in cui bisogna anche rilevare l’angolo di imbardata. Per fare questo esistono i giroscopi, che sono altri strumenti (ben più costosi!) che servono in maniera più specifica a rilevare gli angoli di rotazione.

Un giroscopio elettronico, in realtà, rileva la velocità angolare, poi per successiva integrazione si risale all’angolo.

I giroscopi sono indispensabili sugli elicotteri per evitare la rotazione indesiderata intorno all’asse di rotazione dell’elica principale. Un altro sistema, meno preciso, per rilevare l’angolo di imbardata potrebbe essere quello di utilizzare un magnetometro (una bussola elettronica).

Molto spesso accelerometri, giroscopi e/o magnetometri trovano posto su un unico circuito chiamato IMU (Inertial Measurement Unit – Unità di misurazione inerziale) che permette di tenere sotto controllo qualsiasi aspetto relativo al movimento nello spazio e risulta quindi indispensabile su veicoli a guida autonoma oltre ad un gps (ad esempio sui droni o sugli UAV – Unmanned Aerial Vehicle).

Calcoli per il tilt sensing

Vediamo ora come sfruttare i valori in uscita da un accelerometro per misurare l’angolo di inclinazione. Partiamo con un accelerometro ad un solo asse e immaginiamo di averlo in una condizione iniziale nella quale l’asse X è parallelo all’orizzonte, per cui tutta la forza di gravità è applicata esclusivamente sull’unico asse.

Definiamo con il termine di “orizzonte” il piano perpendicolare alla direzione del vettore rappresentato dalla forza di gravità. Il vettore della forza di gravità è rivolto verso il centro della terra. Quando i vettori di accelerazione hanno lo stesso verso del vettore gravitazionale abbiamo un valore di accelerazione positivo, quando i vettori di accelerazione hanno un verso opposto a quello del vettore gravitazionale abbiamo un valore di accelerazione negativo.

In questo stato di quiete l’accelerometro misura 1g sull’unico asse di misura a disposizione. Supponiamo ora di ruotare l’asse x di un certo angolo θ rispetto al piano dell’orizzonte :

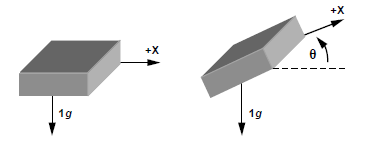
Schematizzando abbiamo in pratica una situazione del genere:

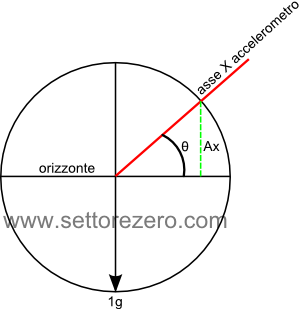
L’asse X dell’accelerometro è inclinato di un angolo θ rispetto all’orizzonte. Il massimo valore di accelerazione di gravità che può agire su un  corpo vale 1g, che rappresenta il raggio della circonferenza.

Questo procedimento di scomposizione è lo stesso che si incontra quando si ha a che fare con il piano inclinato.

La forza che ora agisce sull’asse X dell’accelerometro è rappresentata dal segmento Ax che, in base al primo teorema dei triangoli rettangoli (un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto o per il coseno dell’angolo adiacente) vale precisamente:

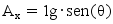
Dato che stiamo ragionando sull’accelerazione statica e 1g è un termine unitario, per mia personale comodità lo ometto nelle descrizioni successive ma dovete tener conto che il valore di 1g è comunque presente, altrimenti da un punto di vista dimensionale è facile commettere degli errori (l’accelerazione è misurata in g, ma il seno di un angolo è un numero neutro, senza dimensioni):

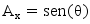
La formula inversa ci permette di ricavare l’angolo θ che l’asse X forma con l’orizzonte:

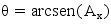
Arcsen è la funzione inversa del seno (arcoseno), e viene spesso anche indicata con sen^-1. Ricordo che θ è misurato in radianti, per avere il valore in gradi basta moltiplicarlo per 180/Π

Utilizzando accelerometri ad un singolo asse, la sensibilità (intesa in questo caso specifico come la variazione del valore in uscita dall’accelerometro in funzione della variazione dell’inclinazione) diminuisce sempre di più man mano che l’angolo aumenta: più ci avvicianiamo a ±90° e più una grande variazione di angolo si traduce in una piccola variazione di accelerazione. Perchè? Questo è evidente dalla (1) : l’accelerazione è direttamente proporzionale al seno dell’angolo di inclinazione per cui di conseguenza la funzione ha un andamento sinusoidale:

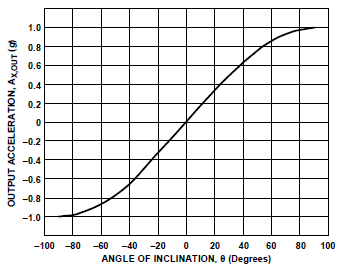
Per apprezzare quindi bene il valore dell’angolo in questi estremi è necessario un accelerometro davvero molto sensibile altrimenti quando siamo prossimi ad un valore di angolo retto, il valore calcolato con la (3) non fornisce un risultato preciso.

Un’altra forte limitazione dovuta all’utilizzo di un accelerometro a singolo asse è data dal fatto che non è possibile misurare valori di accelerazione a 360° dal momento che il valore misurato per un’inclinazione pari a N° è lo stesso valore per un inclinazione pari a 180-N per cui non è possibile distinguere l’inclinazione in un verso o nell’altro. Per alcune applicazioni può anche andar bene, per altre invece no.

Per ovviare a questi “problemi” si ricorre ad un accelerometro a 2 assi ma anche ad un secondo accelerometro a singolo asse ma montato in maniera tale che l’asse di misura sia ortogonale all’asse di misura del primo accelerometro. Nel caso di un accelerometro a due assi, in caso di inclinazione avremo una situazione del genere:

Facciamo di nuovo riferimento alla proiezione dei vettori sulla circonferenza:

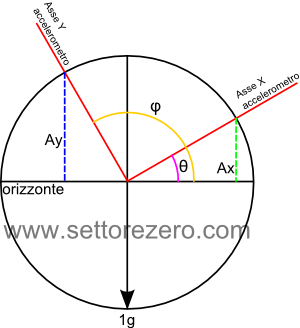
φ è l’angolo che l’asse Y dell’accelerometro forma con l’orizzonte: vale 90°+θ dato che i due assi sono ortogonali tra loro, Ay è l’accelerazione impressa sull’asse Y. Ay può essere calcolato allo stesso modo di Ax considerando l’angolo opposto (che vale 180°-φ, ovvero 90°-θ). Calcolandolo in funzione di θ vediamo che:

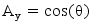
La somma vettoriale di Ax e Ay (non la somma algebrica) deve fornire il valore di 1 (1g). La somma vettoriale di due vettori a e b è data da:

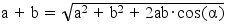
dove con α è indicato l’angolo che i due vettori formano tra loro, in questo caso essendo i due assi ortogonali, il coseno vale zero per cui tutto il termine si annulla e la (5) diventa semplicemente:

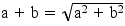
Nel nostro caso al posto di a e b abbiamo i vettori Ax e Ay, la cui somma vettoriale deve fornire 1g di accelerazione, quindi la (6) diventa:

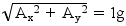
L’introdurre un secondo asse porta ad alcuni vantaggi. Abbiamo detto che con un solo asse la sensibilità diminuisce man mano che ci avviciniamo ad un valore di inclinazione pari a ±90° a causa dell’andamento sinusoidale della relativa funzione, questo continua ad essere vero anche con 2 assi, ma essendo i due assi ortogonali tra loro, quando la sensibilità di un asse diminuisce, la sensibilità dell’altro asse aumenta:

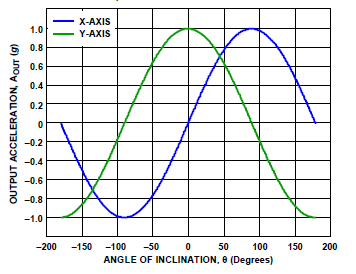
Vedete, ad esempio, nell’intervallo di inclinazione 50 – 100° : la linea blu passa da un valore di 0.8g ad un valore di 1g (una variazione di 0.2g) mentre la linea verde passa da 0.6g a -0.2g (una variazione di 0.8g).

Il valore di accelerazione sull’asse X è proporzionale al seno dell’angolo di inclinazione, mentre il valore di accelerazione sull’asse Y è proporzionale al coseno dell’angolo di inclinazione: le due sensibilità si compensano e il loro rapporto è una costante, per cui possiamo scrivere:

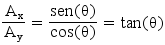
Dalla quale possiamo ricavare il valore di θ:

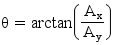
La (9) restituisce un valore di θ molto più preciso rispetto alla (3) dal momento che abbiamo introdotto un secondo asse che ci garantisce una sensibilità costante in tutto l’arco di misura.

L’altro vantaggio di avere 2 assi è quello che ora possiamo distinguere l’inclinazione in tutto l’arco dei 360°:

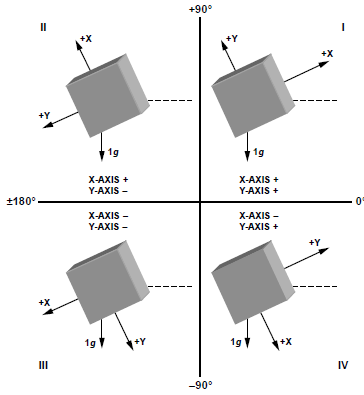
Questo è possibile dal momento che in ogni quadrante i valori di accelerazione anche se possono risultare uguali nel modulo, hanno diverse combinazioni di segno.

Ora passiamo ad un accelerometro a 3 assi. Qui la situazione si fa più complessa ma sicuramente più ricca di informazioni. Misurando i valori di accelerazione sui 3 assi possiamo determinare l’orientamento dell’oggetto nello spazio (questa affermazione non è proprio corretta ma per ora concedetemela):

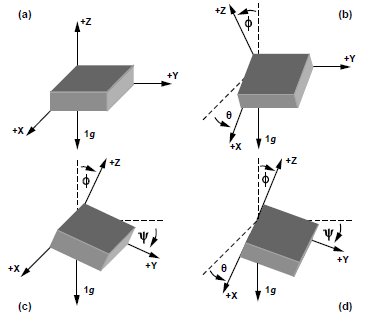
Il nostro oggetto non si muoverà più all’interno di una circonferenza ma all’interno di una sfera: la forza di gravità agisce ora su 3 assi di misura, per cui nei calcoli bisogna tenere conto di tutti e 3 gli assi. Teniamo conto di una posizione iniziale del corpo adagiata sul piano per cui gli assi X e Y del nostro corpo si trovano coricati sull’orizzonte (e quindi formano un angolo di 0° con esso) e l’asse Z è perpendicolare al piano (forma un angolo di 90° con l’orizzonte, o anche di 0° con il vettore di accelerazione gravitazionale).

Qui mi limito esclusivamente a fornire le formule per i calcoli:

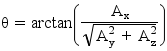
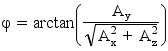
Per l’angolo Φ (che è l’angolo formato dall’asse Z e NO l’angolo di imbardata)  dato che per nostra comodità possiamo prendere come riferimento sia l’orizzonte che il vettore dell’accelerazione gravitazionale, possiamo usare due formule diverse in maniera da calcolare l’angolo rispetto ai due diversi riferimenti:

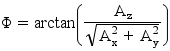
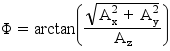
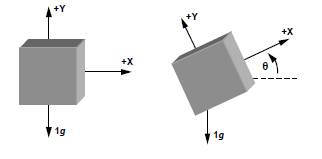
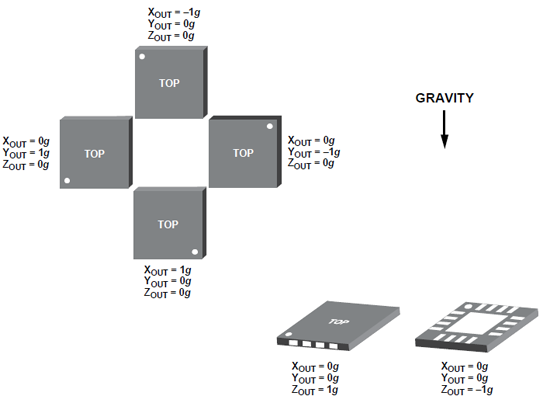
Questa immagine, presente su molti datasheet di accelerometri prodotti dalla Analog Devices, è molto esaustiva e mostra come variano i valori di accelerazione misurati sui 3 assi in dipendenza del posizionamento dell’accelerometro nello spazio:

Gli accelerometri in commercio

Senza parlare della disponibilità di accelerometri a 1, 2 o 3 assi, dato che abbiamo imparato a cosa può servire l’uno o l’altro, per quello che interessa a noi mi limito a dire che gli accelerometri commerciali possono essere di tipo analogico o digitale. Gli accelerometri analogici hanno tante uscite analogiche quanti sono gli assi: un accelerometro a 3 assi avrà quindi 3 uscite. Ogni uscita fornisce un valore in tensione direttamente proporzionale al valore di accelerazione, espresso in g, misurato sul rispettivo asse. Supponendo di avere un accelerometro analogico funzionante a 3V che è in grado di misurare massimo 1g,  abbiamo sugli assi un’ uscita di circa 1.5V quando l’accelerazione vale 0g (valore “centrale”), 3V se vale 1g, 0V se vale -1g.

Gli accelerometri analogici vanno interfacciati con MCU dotate di convertitore A/D e quelli buoni hanno una larghezza di banda selezionabile. Facendo riferimento all’ADXL335 della Analog Devices è possibile settare con un condensatore la larghezza di banda in maniera tale da implementare un filtro passa-basso e quindi ridurre il rumore in uscita e implementare un filtro anti-aliasing sulle uscite. La questione del rumore sulle uscite è tipica di questi dispositivi ed è possibile osservarlo come una continua oscillazione dei valori in uscita dagli assi anche in stato di quiete. Generalmente per ridurre il rumore si ricorre ad elaborate funzioni matematiche come il filtro di Kalman.

Gli accelerometri digitali hanno generalmente una linea di comunicazione seriale I2C o SPI, più raramente abbiamo una UART. In alcuni casi è possibile impostare l’accelerometro perchè utilizzi un protocollo di comunicazione piuttosto che un altro, come l’ADXL345 che può comunicare sia in I2C che in SPI. In questi casi il valore di accelerazione di ogni asse è contenuto in uno o più registri e si interroga quindi l’accelerometro per avere il valore misurato sugli assi.

La scelta dell’uno o dell’altro tipo di accelerometro è dettata unicamente dall’applicazione: se potete “sacrificare” 3 ingressi analogici, l’utilizzo di un accelerometro analogico può forse risultare più semplice.

Ringrazio mio fratello (il mago dell’autocad), Luigi Di Biasi, Mauro Laurenti e Robot-Italy per il supporto nella stesura di questo articolo

Bibliografia

• AN1057 Analog Devices – Using an Accelerometer for Inclination Sensing
• AN3107 Freescale – Measuring tilt with low-g accelerometers
• AN3182 ST Microelectronics – Tilt measurement using a low-g 3-axis accelerometer
• Datasheet ADXL345 – Accelerometro digitale a 3 assi Analog Devices
• Datasheet ADXL335 – Accelerometro analogico a 3 assi Analog Devices
• Acquisto coppia di Nunchuck a buon prezzo
• Acquisto coppia di breakout-boards con ADXL345 a buon prezzo